Abstract
The analysis and interpretation of time series data is of great importance across different fields, including economics, finance, and engineering, among other fields. This kind of data, characterized by sequential observations over time, sometimes exhibits complex patterns and trends that some commonly used models, such as linear autoregressive (AR) and simple moving average (MA) models, cannot capture. This limitation calls for the development of more sophisticated and flexible models that can effectively capture the complexity of time series data. In this study, a more sophisticated model, the Self-Exciting Threshold Autoregressive (SETAR) model, is used to model the Nairobi Securities Exchange (NSE) 20 Share Index, incorporating a Bayesian parameter estimation approach. The objectives of this study are to analyze the properties of the NSE 20 Share Index data, to determine the estimates of SETAR model parameters using the Bayesian approach, to forecast the NSE 20 Share Index for the next 12 months using the fitted model, and to compare the forecasting performance of the Bayesian SETAR with the frequentist SETAR and ARIMA model. Markov Chain Monte Carlo (MCMC) techniques, that is, Gibbs sampling and the Metropolis-Hastings Algorithm, are used to estimate the model parameters. SETAR (2; 4, 4) model is fitted and used to forecast the NSE 20 Share Index. The study's findings generally reveal an upward trajectory in the NSE 20 Share Index starting September 2024. Even though a slight decline is predicted in November, an upward trend is predicted in the following months. On comparing the performance of the models, the Bayesian SETAR model performed better than the linear ARIMA model for both short and longer forecasting horizons. It also performed better than its counterpart model, which uses the frequentist approach for a longer forecasting horizon. These results show the applicability of SETAR modeling in capturing non-linear dynamics. The Bayesian approach incorporated for parameter estimation advanced the model even further by providing a flexible and robust way of parameter estimation and accommodating uncertainty.
Keywords
Nonlinear Time Series, Threshold Autoregressive Models, SETAR, Bayesian Inference, Markov Chain Monte Carlo (MCMC), NSE20 Index
1. Introduction
Over the years, nonlinear time series models have been introduced and developed, with many researchers aiming at capturing the dynamics of time series data. One class of these models is the Threshold Autoregressive (TAR) models first introduced by Tong in 1978. This class of models incorporates regime shifts in time series data, dividing the data into distinct regimes. Each regime has a specific set of parameters that capture the underlying dynamics. Self-Exciting Threshold Autoregressive (SETAR) is an extension of Tong’s TAR, which was proposed to incorporate the concept of self-exciting behavior
. These models consider the past behavior of a series in determining the regime shifts, allowing for the number of regimes to be specified using the data. This feature makes SETAR models a more promising choice in modeling the nonlinear dynamics in time series data like financial data, where the thresholds and number of regimes may change over time. When using SETAR models, there are typically many parameters to be estimated due to the different regimes, and the estimation process can be challenging, especially when the researcher is dealing with high-dimensional or noisy financial data. This requires sophisticated yet flexible and simple approaches, such as the Bayesian approach, to be incorporated into the Self-Exciting Threshold Autoregressive modeling. In this study, the strengths of SETAR models in capturing nonlinear dynamics are combined with the Bayesian approach, which provides a flexible and robust way of parameter estimation that also accommodates uncertainty.
Comparative studies have been done between SETAR and other models, including STAR models, AR models, ARIMA, Seasonal ARIMA, NNETTs, AAR, and LSTAR, among others
| [2] | Aydin D., Güneri Ö. İ. Time Series Prediction Using Hybridization of AR, SETAR and ARM Models. International Journal of Applied. 2015, 5(6), 87-96. |
| [3] | Boero G., Lampis F. The Forecasting Performance of SETAR Models: An Empirical Application. Bulletin of Economic Research. 2017, 69(3), 216-228. https://doi.org/10.1111/boer.12068 |
| [4] | Firat E. H. SETAR (Self-Exciting Threshold Autoregressive) Non-Linear Currency Modelling in EUR/USD, EUR/TRY and USD/TRY Parities. Mathematics and Statistics. 2017, 5(1), 33-55. https://doi.org/10.13189/ms.2017.050105 |
| [5] | Gibson D., Nur D. Threshold Autoregressive Models in Finance: A Comparative Approach. In Proceedings of the Fourth Annual ASEARC Conference, University of Western Sydney, Paramatta, Australia, 2011; 18-23. |
| [6] | Oyewale A. M., Adelekan O. G., Innocient O. O. Forecast Comparison of Seasonal Autoregressive Integrated Moving Average (SARIMA) and Self Exciting Threshold Autoregressive (SETAR) Models. American Journal of Theoretical and Applied Statistics. 2017, 6(6), 278-283. https://doi.org/10.11648/j.ajtas.20170606.13 |
[2-6]
. These studies have shown SETAR models to be an improvement on linear models in regards to capturing volatility. They have also shown that SETAR models have good prediction capabilities. Recently, SETAR models have even been used in a study of COVID-19
| [7] | Tobechukwu N. M., Emmanuel B. O., Ibienebaka B. T. Self-Exciting Threshold Autoregressive Modelling of COVID-19 Confirmed Daily Cases in Nigeria. International Journal of Data Science and Analysis. 2022, 8(6), 182-186. https://doi.org/10.11648/j.ijdsa.20220806.12 |
[7]
. Additionally, studies have investigated the utilization of the Bayesian approach in parameter estimation in TAR models, and it has been established that the approach is effective and feasible in practice
| [8] | Agiwal V., Kumar, J. Bayesian Estimation for Threshold Autoregressive Model with Multiple Structural Breaks. Metron. 2020, 78(3), 361-382. https://doi.org/10.1007/s40300-020-00188-0 |
| [9] | Ojo O. O. Bayesian Modelling of Inflation in Nigeria with Threshold Autoregressive Model. Rattanakosin Journal of Science and Technology. 2021, 3(1), 10-18. |
| [10] | Pan J., Xia Q., Liu J. Bayesian Analysis of Multiple Thresholds Autoregressive Model. Computational Statistics. 2017, 32, 219-237. https://doi.org/10.1007/s00180-016-0673-3 |
[8-10]
. The findings of these studies are promising in regard to the application of SETAR models and the Bayesian framework. In this study, Bayesian SETAR will be used to model and forecast the Nairobi Securities Exchange (NSE) 20 Share index. By combining the flexibility of Bayesian methods with the strengths of SETAR models, this study aims to provide more accurate parameter estimates, enhancing the model’s performance. This has the potential to lead to a more robust and accurate model that will help with decision-making and risk management in the financial market.
2. Materials and Methods
This study focuses on TAR models, particularly SETAR models. The methodology of this study centers on the application of Bayesian Inference to SETAR models.
2.1. Threshold Autoregressive (TAR) Models
Within the framework of threshold time series models, it is assumed that the process has different regimes, determined by a threshold. The basic idea is that the process will behave differently when a variable’s values go beyond a certain threshold, meaning that different models apply when the values are below and above the threshold.
Suppose a series
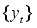
is observed at discrete time points t. TAR(p), a TAR model of order
p and two regimes can be written as
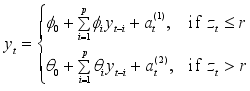 (1)
(1) where
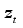
is the threshold variable, and
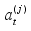
are independent Gaussian white noise processes with mean zero and variance
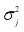
, with j = 1,2.
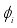
and
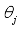
are real-valued parameters and
r is the threshold.
SETAR model is a type of TAR models. Considering the above TAR model with two regimes (
1), if the
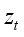
value is replaced with previous values of the time series
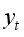
as below, the TAR model is then referred to as SETAR model.
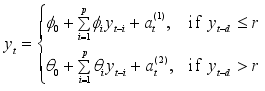 (2)
(2) The switch of regimes is therefore influenced by the past values of
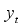
, that is,
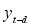
, where
d represents the delay parameter.
The SETAR model can be generalized to include multiple regimes. Let
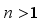
be a positive finite integer and
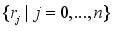
a real number sequence with
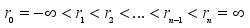
where
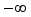
and
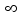
are regarded as real numbers. Then a time series
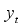
is a
m-regime SETAR (p) model if it satisfies
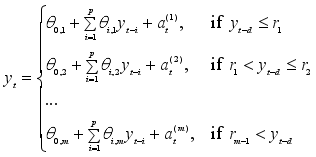 (3)
(3) where
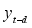
is the threshold variable and
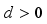
is the delay parameter.
In SETAR models, there exists many free parameters that need to be chosen and approximated in building the models. These parameters include the number of regimes/ thresholds, threshold values, orders of the AR models, and the model coefficients. The Bayesian approach provides a promising way of estimating the model parameters.
2.2. Bayesian Estimation of the Model Parameters
In the Bayesian statistical perspective, parameters are viewed as random variables to account for uncertainty in their values. Bayesian analysis involves specifying a likelihood, which is the conditional density of data given the parameters, together with a prior distribution for the parameters derived from past knowledge or beliefs. The joint density of data and parameters is obtained by multiplying the prior and likelihood. To get the marginal density of the data, the parameters have to be integrated out. The posterior density, which represents the parameters given the data, is then derived by dividing the joint density by the marginal density. This posterior contains all the information about parameter values and serves as the foundation for Bayesian inference.
Suppose
m observations
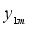
are collected of a time series
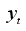
. Suppose that each data point,
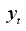
, is associated with a probability distribution which can be expressed as a function of a parameter or many parameters
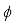
so that the relationship between
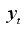
and
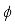
is described by a pdf
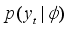
. When
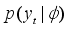
is considered as a function of
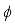
instead of
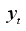
, it is referred to as the
likelihood function. By applying Bayes' theorem, the posterior pdf
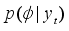
can be derived, that is, the posterior pdf of
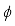
given
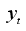
, by multiplying the likelihood with the prior density,
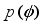
. That is,
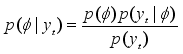 (4)
(4) where
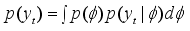
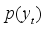
defines what is known as predictive density function. The prior distribution provides a means to include researcher's initial beliefs or assumptions regarding
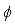
, and Bayes' theorem enables the revision and updating of these assumptions once the data is observed.
2.2.1. Obtaining Priors
For this study, conjugate priors will be used. The natural conjugate priors are selected as follows;
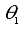
and
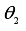
are taken as independent and normally distributed as
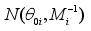
, while
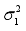
and
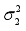
are taken as independent with inverse gamma distribution
inverse gamma 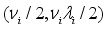
. The hyper-parameters d and r are assumed to be known.
r is presumed to have a uniform distribution on
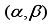
while
d is presumed to take a discrete uniform distribution on
1,2,..., D.
2.2.2. Obtaining Posterior Distributions
The primary interest of the analysis is to obtain the marginal posterior distributions of the parameters
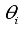
's,
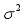
s,
r, and
d. Determining the posterior distribution is frequently achallenging task due to the need for complex numerical integration in high-dimensional spaces. Therefore, Gibbs Sampler and the Metropolis-Hastings algorithm will be used in this study to find the conditional posterior distributions of the unknown parameters.
(i). Gibbs Sampler
The Gibbs sampler, which is a Markov Chain Monte Carlo (MCMC) technique, is used to estimate target posterior distributions from conditional distributions. Gibbs Sampling is specifically designed to sample from multivariate distributions by sequentially updating each variable while conditioning on the current values of the other variables.
Consider a scenario where the random variable
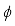
can be broken down into components
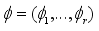
and the conditional densities
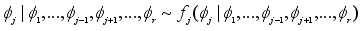
can be simulated for
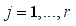
. Then, to sample from the joint density of
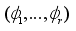
using Gibbs sampler, the following algorithm is followed:
1. Given the sample
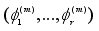
, generate
2.
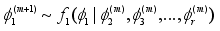
,
3.
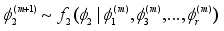
,
.
.
.
r.
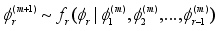
.
The conditional densities of the unknown parameters can be derived except for the conditional density of r. Therefore, these conditional distributions will be used alongside the Gibbs sampling technique described above to obtain the marginal posterior distributions for the unknown parameters. Regarding r, the Metropolis algorithm will be used.
(ii). The Metropolis-Hastings Algorithm
For r, the conditional posterior probability function is
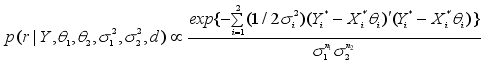 (5)
(5) with
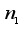
and
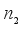
being functions of
r.
Let the conditional density above (5) be denoted by
f(k), and as before, the assumption that
k's prior distribution is uniform over
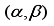
is made. Hence, a transition kernel
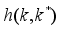
with
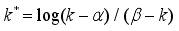
can be utilized to map
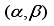
into
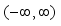
. The Metropolis algorithm will then work in the following manner;
1. Begin with an initial value,
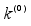
drawn from the prior
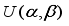
and set the indicator
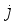
to 0.
2. Utilizing the transition kernel
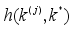
, generate a new point
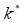
.
3. With a probability of
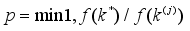
, update
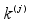
to
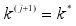
and remain at
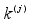
with a probability of
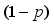
.
4. By increasing the indicator, repeat steps 2 and 3 until a stationary distribution is attained.
2.3. Test for Linearity
SETAR models were introduced to handle non-linear time series data, and hence, before proceeding with modeling, it is essential to check for non-linearity to ensure the model selected is appropriate. The non-linearity tests that will be used are Tsay’s F test and BDS test.
2.3.1. Tsay’s F Test
In Tsay’s F test, the null hypothesis of linearity is tested against the alternative hypothesis that there exists a threshold model.
Considering a TAR(p) process with two regimes, the test is,
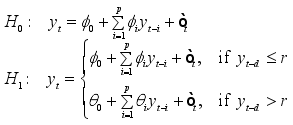 (6)
(6) 2.3.2. BDS Test for Nonlinearity
The BDS test investigates the spatial dependence of a time series. The series is represented in a multi-dimensional space (m-space), and the dependence of x is investigated by counting close points, which are data points that are within a distance of ’eps’ from each other.
H0: The data is independently and identically distributed (iid).
H1: The residuals exhibit an underlying structure, potentially of a non-linear nature.
2.4. Test for Stationarity
Stationarity tests assess whether the time series is stationary, i.e, whether it exhibits stable statistical properties over time, including the mean, variance, and autocorrelation. Many time series models, Autoregressive models included, assume stationarity as it simplifies the analysis and allows for more reliable forecasts. The stationarity tests that will be employed are the ADF Test and the Zivot and Andrews (1992) test.
2.4.1. ADF Test
ADF test tests for the existence of unit roots in the data, which are indicators of non-stationarity. The ADF test's null hypothesis suggests that the time series possesses unit roots, rendering it non-stationary, while the alternative hypothesis suggests the absence of unit roots, indicating stationarity.
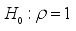
(hasunitroots)
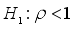
(nounitroots)
2.4.2. Zivot-Andrews Unit Root Test
The null hypothesis is that the time series represents an integrated process devoid of structural changes. Conversely, the alternative hypothesis proposes that the process is trend-stationary, characterized by a singular break occurring at an unspecified moment in time.
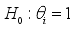
(serieshasaunitrootwithdrift)
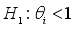
(seriesisstationarywithbreak(s))
3. Results
3.1. Data
The data that is utilized in this study is the NSE 20 Share Index historical data from December 1997 to August 2024. The NSE 20 Share Index is basically a price-weighted Index, which is calculated as the mean of the top 20 best-performing companies in Kenya. The NSE20 Index generally tracks the performance of the 20 largest and best-performing companies listed on the Nairobi Securities Exchange (NSE) in Kenya.
Figure 1 below shows the data. The time series is asymmetrical, and this insinuates a lack of stable statistical properties, which is a challenge when doing estimation with both linear and non-linear models.
Figure 1. Time Series of NSE 20 share index monthly: Dec 1997 - Aug 2024.
3.2. Non-Linearity Test
3.2.1. Tsay’s F-Test
Tsay's threshold non-linearity test is conducted using different working orders (1 to 10). The following table shows the results of the tests showing the order of the model used for testing, the F test statistic, and the p-value obtained.
Table 1. Test for Threshold Non-Linearity using Tsay’s F-Test.
Working Orders | Test statistic | P-value |
1 | 1.246 | 0.2652 |
2 | 1.871 | 0.1345 |
3 | 1.671 | 0.1276 |
4 | 1.59 | 0.1085 |
5 | 1.634 | 0.06407 |
6 | 2.272 | 0.001457 |
7 | 2.453 | 0.000116 |
8 | 2.273 | 0.0001182 |
9 | 2.18 | 8.27e-05 |
10 | 2.273 | 1.068e-05 |
The results support threshold non-linearity when orders 6, 7, 8, 9, and 10 are used. Therefore, at 5% level of significance, the null hypothesis that suggests linearity is rejected.
3.2.2. BDS Test
The results obtained from running the BDS test are as shown below.
Table 2. Test for Non-Linearity using BDS Test.
P-values |
Embedding Dimension | ε (standard deviation) |
| 0.5 | 1.0 | 1.5 | 2.0 |
2 | 2.2 e-16 | 2.2 e-16 | 2.2 e-16 | 2.2 e-16 |
3 | 2.2 e-16 | 2.2 e-16 | 2.2 e-16 | 2.2 e-16 |
From the results, the null hypothesis, stating that the data is i.i.d is rejected for all m and ε combinations at the standard significance levels. Given the lack of apparent linear patterns in the data, the outcomes of the BDS test indicate nonlinear structures within the data.
3.3. Test for Stationarity
The ADF test yields a p-value of 0.6862, leading to the retention of the null hypothesis, as the obtained p-value exceeds the 0.05 significance level. Upon running the Zivot-Andrews Unit Root Test, the t-statistic of the Z-A test exceeds the critical values, leading to the retention of the null hypothesis, signifying the presence of a unit root in the time series. Both tests imply that the time series is non-stationary.
The time series data is non-stationary, and hence, it will be transformed to stationarity by logarithmic transformation of the series and then differencing. The following is the transformed time series.
Figure 2. Time Series of Change in NSE 20 Share Index.
After logarithmic transformation followed by differencing, stationarity of the series is tested again and the results show that the series is now stationary.
3.4. Selection of Regimes and the Orders for the Regimes
Looking at
Figure 2, positive values indicate growth in the NSE20 Index, which can be interpreted as good health or performance of the Kenyan stock market, while negative values and values close to zero indicate poor performance or stagnation. With these observations, a two-regime model will be used to model these growths and declines. This translates to just one
r value, which can informally be envisioned as a horizontal line separating the growth from the drop seasons. Therefore, the SETAR model will have two regimes and will take the form
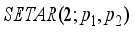
.
To develop the SETAR model, we need to find the orders of the two models, for the two identified regimes, p
1 and p
2, and the lag parameter d. We use ACF and PACF to get the lag order. From the ACF and PACF plots
Figure 3 and
Figure 4 below, an order of 4 will be used for both models.
3.5. Bayesian Parameter Estimation
Next, the unknown parameters
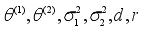
are estimated using the Bayesian approach. The Gibbs sampler was executed for 1,000 iterations, and the initial 500 iterations were disregarded as the burn-in sample. The estimates of the parameters alongside their standard errors are as shown in the table below;
Table 3. Parameter Estimation for the SETAR Model.
Parameter | Mean | Median | Standard Deviation |

| -0.0332 | -0.0327 | 0.0109 |

| -0.2871 | -0.2894 | 0.1590 |

| 0.0739 | 0.0677 | 0.1353 |

| -0.0866 | -0.0818 | 0.1369 |

| 0.3277 | 0.3282 | 0.1194 |

| 0.0023 | 0.0020 | 0.0042 |

| 0.1288 | 0.1301 | 0.0963 |

| 0.0532 | 0.0566 | 0.0584 |

| 0.1191 | 0.1162 | 0.0593 |

| 0.0616 | 0.0607 | 0.0668 |

| 0.0033 | 0.0032 | 0.0005 |

| 0.0024 | 0.0024 | 0.0002 |
r | -0.0218 | -0.0215 | 0.0037 |
d | 1 | 1 | 0.0000 |
Using the above results, the following model is obtained;
where
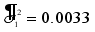
and
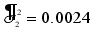
. The estimated value of
d is 1.
3.6. Forecasting
Next, the SETAR model obtained above will be used to predict future values of the NSE20. To gauge the effectiveness of the Bayesian SETAR model, its forecasting performance is compared with that of a SETAR model estimated through a frequentist approach and an ARIMA model.
3.6.1. Forecasting with the Bayesian SETAR (2;4,4) Model
For the forecasting process, the one-step-ahead recursive method was employed. This method involves a step-by-step prediction process, where the first forecast is initiated by estimating the next value using our Bayesian SETAR (2;4,4) model. Subsequently, this predicted value is integrated into the existing data, and the model is re-estimated. This cycle continues, step by step, to predict future values.
NSE 20 Share Index values for the next 12 months starting from September 2024 to August 2025 forecasted using the Bayesian SETAR model are as shown in
Figure 5 and
Table 4 below.
Figure 5. Predicted Future Changes of the NSE20 Index Are Indicated by the Red line.
Table 4. Predicted Values of the NSE 20 Share Index for September 2024 to August 2025.
Predictions |
Month/Year | Mean | Lower | Upper |
Sep 2024 | 1683.5889 | 1661.17926 | 1703.74326 |
Oct 2024 | 1689.9987 | 1667.50375 | 1711.25625 |
Nov 2024 | 1665.6705 | 1613.37418 | 1688.30953 |
Dec 2024 | 1671.6777 | 1645.47278 | 1692.53558 |
Jan 2025 | 1677.5389 | 1654.05153 | 1697.62081 |
Feb 2025 | 1684.2624 | 1661.51153 | 1707.66638 |
Mar 2025 | 1693.7208 | 1664.00567 | 1738.85656 |
Apr 2025 | 1698.9795 | 1676.19736 | 1719.14616 |
May 2025 | 1704.7658 | 1680.7292 | 1723.79413 |
June 2025 | 1713.6537 | 1685.10479 | 1753.52448 |
Jul 2025 | 1718.9743 | 1697.45106 | 1739.20437 |
Aug 2025 | 1723.9665 | 1700.33918 | 1743.90657 |
3.6.2. Evaluation of the Model's Forecasting Ability
In evaluating the forecasting precision of the model, the Bayesian SETAR model, developed with data from January 1998 to December 2023, was compared with a SETAR model estimated using the frequentist approach and an ARIMA model. The primary interest was forecasting the NSE 20 Share Index changes from January 2024 to August 2024. To assess the accuracy of these forecasts, Root Mean Square Errors (RMSE) were calculated for the three models. The results are as follows;
Table 5. RMSE for the Bayesian SETAR, Normal SETAR, and ARIMA Models (8 Months).
| Bayesian SETAR | Frequentist SETAR | ARIMA |
RMSE | 0.05074525 | 0.04949407 | 0.05102666 |
From the above results, the Bayesian SETAR model outperformed ARIMA, even though its frequentist counterpart performed best in forecasting the NSE20 changes for a short period (eight months). Next, a comparison is made for a longer forecasting horizon, where structural breaks are expected. The models were fitted for data from January 1998 to Aug 2019, and forecasts were made for September 2019 to August 2024 (60 months). The performance results are as follows;
Table 6. RMSE for the Bayesian SETAR, Normal SETAR, and ARIMA Models (60 Months).
| Bayesian SETAR | Frequentist SETAR | ARIMA |
RMSE | 0.03947424 | 0.05351723 | 0.04191522 |
Figure 6. Original Data and Forecasted Values using Bayesian SETAR and using ARIMA.
For a longer forecasting horizon, the Bayesian SETAR had a better predictive power.
4. Discussion
The effectiveness of SETAR models in capturing non-linear dynamics has been demonstrated in prior studies. In one study, for instance, it was found that the SETAR (2,2,1) model outperformed an ARIMA (3,1,3) model for modeling crude oil production fluctuations, underscoring SETAR's capability to capture complex, non-linear patterns more effectively than traditional linear models
| [11] | Onyeka-Ubaka J. N., Ebiringa O. A. Self-exciting Threshold Autoregressive Model with Application to Crude Oil Production in Nigeria. Asian Journal of Probability and Statistics. 2023, 22(1), 1-18. https://doi.org/10.9734/ajpas/2023/v22i1473 |
[11]
. Another study highlighted that SETAR models could better depict the dynamics of the US public debt-to-GDP ratio over several decades, outperforming other threshold models like ESTAR and LSTAR, particularly in reflecting shifts before and after major economic events such as the Global Financial Crisis
| [12] | Andric V., Bodroza D., Djukic M. A Commentary on US Sovereign Debt Persistence and Nonlinear Fiscal Adjustment. Mathematics. 2024, 12(20), 3250. https://doi.org/10.3390/math12203250 |
[12]
. While these studies, among others
| [2] | Aydin D., Güneri Ö. İ. Time Series Prediction Using Hybridization of AR, SETAR and ARM Models. International Journal of Applied. 2015, 5(6), 87-96. |
| [3] | Boero G., Lampis F. The Forecasting Performance of SETAR Models: An Empirical Application. Bulletin of Economic Research. 2017, 69(3), 216-228. https://doi.org/10.1111/boer.12068 |
| [4] | Firat E. H. SETAR (Self-Exciting Threshold Autoregressive) Non-Linear Currency Modelling in EUR/USD, EUR/TRY and USD/TRY Parities. Mathematics and Statistics. 2017, 5(1), 33-55. https://doi.org/10.13189/ms.2017.050105 |
| [5] | Gibson D., Nur D. Threshold Autoregressive Models in Finance: A Comparative Approach. In Proceedings of the Fourth Annual ASEARC Conference, University of Western Sydney, Paramatta, Australia, 2011; 18-23. |
| [6] | Oyewale A. M., Adelekan O. G., Innocient O. O. Forecast Comparison of Seasonal Autoregressive Integrated Moving Average (SARIMA) and Self Exciting Threshold Autoregressive (SETAR) Models. American Journal of Theoretical and Applied Statistics. 2017, 6(6), 278-283. https://doi.org/10.11648/j.ajtas.20170606.13 |
[2-6]
, have demonstrated the capabilities of SETAR models, they primarily utilized frequentist approaches for parameter estimation, which does not fully accommodate uncertainty in parameter estimation. Hence, this study expands on this to explore the utilization of the Bayesian approach for parameter estimation in SETAR models.
Bayesian analysis that utilizes prior information will often give better inference compared to frequentist analysis that ignores prior information
. Recently, Bayesian time series analysis techniques have been widely applied to solve different problems
| [14] | Bisaglia L., Canale A. Bayesian Nonparametric Forecasting for INAR Models. Computational Statistics & Data Analysis. 2016, 100, 70-78. https://doi.org/10.1016/j.csda.2014.12.011 |
| [15] | Drovandi C. C., Pettitt A. N., McCutchan R. A. Exact and Approximate Bayesian Inference for Low Integer-Valued Time Series Models with Intractable Likelihoods. 2016, 11(2) 325 - 352. https://doi.org/10.1214/15-BA950 |
| [16] | Li Y., Yu J., Zeng T. Deviance Information Criterion for Latent Variable Models and Misspecified Models. Journal of econometrics. 2020, 216(2), 450-493. https://doi.org/10.1016/j.jeconom.2019.11.002 |
| [17] | Yang K., Li H., Wang D. Estimation of Parameters in the Self-Exciting Threshold Autoregressive Processes for Nonlinear Time Series of Counts. Applied Mathematical Modelling. 2018, 57, 226-247. https://doi.org/10.1016/j.apm.2018.01.003 |
[14-17]
. However, the integration of Bayesian techniques into SETAR models and their application is still an emerging area, and hence, this study sought to fill this gap in the literature by applying the approach to the NSE20 share index.
The NSE20 time series data was explored for attributes including stationarity and linearity, which, in turn, laid the groundwork for fitting a SETAR model. The data portrayed non-linearity, making the SETAR model suitable for modeling the data. Through an analysis of the data, SETAR (2;4,4) was the most adequate for the data. Using the Bayesian approach, the model parameters were estimated, including autoregressive coefficients θ(1) and θ(2), regime-switching parameter (r), error variances, and the delay parameter (d). The estimated Bayesian SETAR model was then used to generate forecasts for the next 12 months of the NSE20 Index. Considering the forecasts obtained, the NSE 20 Share Index is expected to generally continue upward in the coming months, even though a slight drop is predicted for November, followed by an upward trajectory. The implications of these findings extend to different stakeholders in the financial market, including investors, investment firms, and policymakers.
On forecasting performance, the Bayesian SETAR model outperformed both the SETAR model utilizing the Frequentist approach and the ARIMA model for a longer forecasting horizon and during periods characterized by high fluctuations. Additionally, in both cases (short and long forecasting horizons, Bayesian SETAR outperformed ARIMA, a commonly used linear model. These findings underscore the Bayesian SETAR model's resilience and adaptability, particularly in scenarios characterized by volatility. Additionally, the findings of this study highlight the applicability of SETAR modeling in capturing the nonlinear dynamics inherent in financial time series data. The results highlight the advantages of incorporating Bayesian techniques for modeling and forecasting nonlinear financial time series. On top of providing a flexible and robust way of parameter estimation, the inclusion of the Bayesian approach provides a way of incorporating uncertainty.
Future research can extend this study's comparison to include other nonlinear time series models. Additionally, natural conjugate priors were chosen for mathematical convenience in this study. Hence, future studies can also investigate how variations in prior distributions for the model parameters affect the results. Two regimes were also selected for the study. Future studies can extend the study to incorporate more than two regimes. Expanding the scope to include multi-regimes may better capture the data's underlying patterns and nonlinear relationships that may not be fully revealed in a two-regime framework.
5. Conclusions
In conclusion, the findings of this study highlight the applicability of SETAR modeling in capturing the non-linear dynamics inherent in financial time series data. The Bayesian SETAR model, specifically, exhibited superior performance, particularly in scenarios marked by high volatility and fluctuations and for a longer forecasting horizon by outperforming its counterparts. This underscores the model’s resilience and adaptability, positioning it as a robust tool for forecasting in financial environments characterized by dynamic and unpredictable changes. Its ability to handle non-linearities and volatile conditions suggests practical applications in decision-making processes, risk management, and strategic planning within the financial sector. As the Kenyan financial market continues to navigate complex and evolving conditions, the Bayesian SETAR model emerges as a valuable asset for stakeholders seeking reliable insights into market behavior and trends.
Abbreviations
SETAR | Self-Exciting Threshold Autoregressive |
NSE | Nairobi Securities Exchange |
NSE20 | NSE 20 Share Index |
pdf | Probability Density Function |
AR | Autoregressive |
MA | Moving Average |
ARIMA | Autoregressive Integrated Moving Average |
i.i.d | Independently and Identically Distributed |
Author Contributions
Jacinta Muindi: Conceptualization, Data Curation, Formal Analysis, Investigation, Methodology, Software, Validation, Visualization, Writing – original draft, Writing – review & editing
Ronald Wanyonyi: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing – review & editing
George Muhua: Conceptualization, Data curation, Formal Analysis, Investigation, Methodology, Validation, Visualization, Writing – review & editing
Funding
This work is not supported by any external funding.
Data Availability Statement
The data is available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
| [1] |
Tong H., Lim K. S., Threshold Autoregression, Limit Cycles and Cyclical Data. Journal of the Royal Statistical Society: Series B (Methodological). 1980, 42(3), 245-268.
https://doi.org/10.1111/j.2517-6161.1980.tb01126.x
|
| [2] |
Aydin D., Güneri Ö. İ. Time Series Prediction Using Hybridization of AR, SETAR and ARM Models. International Journal of Applied. 2015, 5(6), 87-96.
|
| [3] |
Boero G., Lampis F. The Forecasting Performance of SETAR Models: An Empirical Application. Bulletin of Economic Research. 2017, 69(3), 216-228.
https://doi.org/10.1111/boer.12068
|
| [4] |
Firat E. H. SETAR (Self-Exciting Threshold Autoregressive) Non-Linear Currency Modelling in EUR/USD, EUR/TRY and USD/TRY Parities. Mathematics and Statistics. 2017, 5(1), 33-55.
https://doi.org/10.13189/ms.2017.050105
|
| [5] |
Gibson D., Nur D. Threshold Autoregressive Models in Finance: A Comparative Approach. In Proceedings of the Fourth Annual ASEARC Conference, University of Western Sydney, Paramatta, Australia, 2011; 18-23.
|
| [6] |
Oyewale A. M., Adelekan O. G., Innocient O. O. Forecast Comparison of Seasonal Autoregressive Integrated Moving Average (SARIMA) and Self Exciting Threshold Autoregressive (SETAR) Models. American Journal of Theoretical and Applied Statistics. 2017, 6(6), 278-283.
https://doi.org/10.11648/j.ajtas.20170606.13
|
| [7] |
Tobechukwu N. M., Emmanuel B. O., Ibienebaka B. T. Self-Exciting Threshold Autoregressive Modelling of COVID-19 Confirmed Daily Cases in Nigeria. International Journal of Data Science and Analysis. 2022, 8(6), 182-186.
https://doi.org/10.11648/j.ijdsa.20220806.12
|
| [8] |
Agiwal V., Kumar, J. Bayesian Estimation for Threshold Autoregressive Model with Multiple Structural Breaks. Metron. 2020, 78(3), 361-382.
https://doi.org/10.1007/s40300-020-00188-0
|
| [9] |
Ojo O. O. Bayesian Modelling of Inflation in Nigeria with Threshold Autoregressive Model. Rattanakosin Journal of Science and Technology. 2021, 3(1), 10-18.
|
| [10] |
Pan J., Xia Q., Liu J. Bayesian Analysis of Multiple Thresholds Autoregressive Model. Computational Statistics. 2017, 32, 219-237.
https://doi.org/10.1007/s00180-016-0673-3
|
| [11] |
Onyeka-Ubaka J. N., Ebiringa O. A. Self-exciting Threshold Autoregressive Model with Application to Crude Oil Production in Nigeria. Asian Journal of Probability and Statistics. 2023, 22(1), 1-18.
https://doi.org/10.9734/ajpas/2023/v22i1473
|
| [12] |
Andric V., Bodroza D., Djukic M. A Commentary on US Sovereign Debt Persistence and Nonlinear Fiscal Adjustment. Mathematics. 2024, 12(20), 3250.
https://doi.org/10.3390/math12203250
|
| [13] |
Bolstad W. M., Curran J. M. Introduction to Bayesian statistics. John Wiley & Sons. 2016, 237-253.
https://doi.org/10.1002/9781118593165
|
| [14] |
Bisaglia L., Canale A. Bayesian Nonparametric Forecasting for INAR Models. Computational Statistics & Data Analysis. 2016, 100, 70-78.
https://doi.org/10.1016/j.csda.2014.12.011
|
| [15] |
Drovandi C. C., Pettitt A. N., McCutchan R. A. Exact and Approximate Bayesian Inference for Low Integer-Valued Time Series Models with Intractable Likelihoods. 2016, 11(2) 325 - 352.
https://doi.org/10.1214/15-BA950
|
| [16] |
Li Y., Yu J., Zeng T. Deviance Information Criterion for Latent Variable Models and Misspecified Models. Journal of econometrics. 2020, 216(2), 450-493.
https://doi.org/10.1016/j.jeconom.2019.11.002
|
| [17] |
Yang K., Li H., Wang D. Estimation of Parameters in the Self-Exciting Threshold Autoregressive Processes for Nonlinear Time Series of Counts. Applied Mathematical Modelling. 2018, 57, 226-247.
https://doi.org/10.1016/j.apm.2018.01.003
|
Cite This Article
-
APA Style
Muindi, J., Muhua, G., Wanyonyi, R. (2024). Self-Exciting Threshold Autoregressive (SETAR) Modelling of the NSE 20 Share Index Using the Bayesian Approach. American Journal of Theoretical and Applied Statistics, 13(6), 203-212. https://doi.org/10.11648/j.ajtas.20241306.13
 Copy
|
Copy
|
 Download
Download
ACS Style
Muindi, J.; Muhua, G.; Wanyonyi, R. Self-Exciting Threshold Autoregressive (SETAR) Modelling of the NSE 20 Share Index Using the Bayesian Approach. Am. J. Theor. Appl. Stat. 2024, 13(6), 203-212. doi: 10.11648/j.ajtas.20241306.13
 Copy
|
Copy
|
 Download
Download
AMA Style
Muindi J, Muhua G, Wanyonyi R. Self-Exciting Threshold Autoregressive (SETAR) Modelling of the NSE 20 Share Index Using the Bayesian Approach. Am J Theor Appl Stat. 2024;13(6):203-212. doi: 10.11648/j.ajtas.20241306.13
 Copy
|
Copy
|
 Download
Download
-
@article{10.11648/j.ajtas.20241306.13,
author = {Jacinta Muindi and George Muhua and Ronald Wanyonyi},
title = {Self-Exciting Threshold Autoregressive (SETAR) Modelling of the NSE 20 Share Index Using the Bayesian Approach
},
journal = {American Journal of Theoretical and Applied Statistics},
volume = {13},
number = {6},
pages = {203-212},
doi = {10.11648/j.ajtas.20241306.13},
url = {https://doi.org/10.11648/j.ajtas.20241306.13},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajtas.20241306.13},
abstract = {The analysis and interpretation of time series data is of great importance across different fields, including economics, finance, and engineering, among other fields. This kind of data, characterized by sequential observations over time, sometimes exhibits complex patterns and trends that some commonly used models, such as linear autoregressive (AR) and simple moving average (MA) models, cannot capture. This limitation calls for the development of more sophisticated and flexible models that can effectively capture the complexity of time series data. In this study, a more sophisticated model, the Self-Exciting Threshold Autoregressive (SETAR) model, is used to model the Nairobi Securities Exchange (NSE) 20 Share Index, incorporating a Bayesian parameter estimation approach. The objectives of this study are to analyze the properties of the NSE 20 Share Index data, to determine the estimates of SETAR model parameters using the Bayesian approach, to forecast the NSE 20 Share Index for the next 12 months using the fitted model, and to compare the forecasting performance of the Bayesian SETAR with the frequentist SETAR and ARIMA model. Markov Chain Monte Carlo (MCMC) techniques, that is, Gibbs sampling and the Metropolis-Hastings Algorithm, are used to estimate the model parameters. SETAR (2; 4, 4) model is fitted and used to forecast the NSE 20 Share Index. The study's findings generally reveal an upward trajectory in the NSE 20 Share Index starting September 2024. Even though a slight decline is predicted in November, an upward trend is predicted in the following months. On comparing the performance of the models, the Bayesian SETAR model performed better than the linear ARIMA model for both short and longer forecasting horizons. It also performed better than its counterpart model, which uses the frequentist approach for a longer forecasting horizon. These results show the applicability of SETAR modeling in capturing non-linear dynamics. The Bayesian approach incorporated for parameter estimation advanced the model even further by providing a flexible and robust way of parameter estimation and accommodating uncertainty.
},
year = {2024}
}
 Copy
|
Copy
|
 Download
Download
-
TY - JOUR
T1 - Self-Exciting Threshold Autoregressive (SETAR) Modelling of the NSE 20 Share Index Using the Bayesian Approach
AU - Jacinta Muindi
AU - George Muhua
AU - Ronald Wanyonyi
Y1 - 2024/11/26
PY - 2024
N1 - https://doi.org/10.11648/j.ajtas.20241306.13
DO - 10.11648/j.ajtas.20241306.13
T2 - American Journal of Theoretical and Applied Statistics
JF - American Journal of Theoretical and Applied Statistics
JO - American Journal of Theoretical and Applied Statistics
SP - 203
EP - 212
PB - Science Publishing Group
SN - 2326-9006
UR - https://doi.org/10.11648/j.ajtas.20241306.13
AB - The analysis and interpretation of time series data is of great importance across different fields, including economics, finance, and engineering, among other fields. This kind of data, characterized by sequential observations over time, sometimes exhibits complex patterns and trends that some commonly used models, such as linear autoregressive (AR) and simple moving average (MA) models, cannot capture. This limitation calls for the development of more sophisticated and flexible models that can effectively capture the complexity of time series data. In this study, a more sophisticated model, the Self-Exciting Threshold Autoregressive (SETAR) model, is used to model the Nairobi Securities Exchange (NSE) 20 Share Index, incorporating a Bayesian parameter estimation approach. The objectives of this study are to analyze the properties of the NSE 20 Share Index data, to determine the estimates of SETAR model parameters using the Bayesian approach, to forecast the NSE 20 Share Index for the next 12 months using the fitted model, and to compare the forecasting performance of the Bayesian SETAR with the frequentist SETAR and ARIMA model. Markov Chain Monte Carlo (MCMC) techniques, that is, Gibbs sampling and the Metropolis-Hastings Algorithm, are used to estimate the model parameters. SETAR (2; 4, 4) model is fitted and used to forecast the NSE 20 Share Index. The study's findings generally reveal an upward trajectory in the NSE 20 Share Index starting September 2024. Even though a slight decline is predicted in November, an upward trend is predicted in the following months. On comparing the performance of the models, the Bayesian SETAR model performed better than the linear ARIMA model for both short and longer forecasting horizons. It also performed better than its counterpart model, which uses the frequentist approach for a longer forecasting horizon. These results show the applicability of SETAR modeling in capturing non-linear dynamics. The Bayesian approach incorporated for parameter estimation advanced the model even further by providing a flexible and robust way of parameter estimation and accommodating uncertainty.
VL - 13
IS - 6
ER -
 Copy
|
Copy
|
 Download
Download
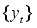 is observed at discrete time points t. TAR(p), a TAR model of order p and two regimes can be written as
is observed at discrete time points t. TAR(p), a TAR model of order p and two regimes can be written as 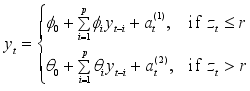 (1)
(1) 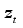 is the threshold variable, and
is the threshold variable, and 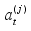 are independent Gaussian white noise processes with mean zero and variance
are independent Gaussian white noise processes with mean zero and variance 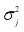 , with j = 1,2.
, with j = 1,2. 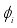 and
and 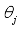 are real-valued parameters and r is the threshold.
are real-valued parameters and r is the threshold. 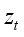 value is replaced with previous values of the time series
value is replaced with previous values of the time series 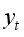 as below, the TAR model is then referred to as SETAR model.
as below, the TAR model is then referred to as SETAR model. 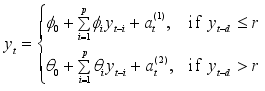 (2)
(2)  , that is,
, that is,  , where d represents the delay parameter.
, where d represents the delay parameter. 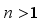 be a positive finite integer and
be a positive finite integer and 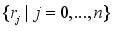 a real number sequence with
a real number sequence with 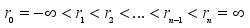 where
where 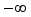 and
and 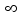 are regarded as real numbers. Then a time series
are regarded as real numbers. Then a time series 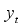 is a m-regime SETAR (p) model if it satisfies
is a m-regime SETAR (p) model if it satisfies 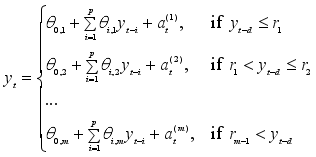 (3)
(3) 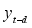 is the threshold variable and
is the threshold variable and 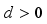 is the delay parameter.
is the delay parameter. 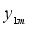 are collected of a time series
are collected of a time series 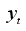 . Suppose that each data point,
. Suppose that each data point, 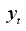 , is associated with a probability distribution which can be expressed as a function of a parameter or many parameters
, is associated with a probability distribution which can be expressed as a function of a parameter or many parameters 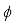 so that the relationship between
so that the relationship between 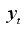 and
and 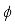 is described by a pdf
is described by a pdf 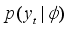 . When
. When 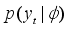 is considered as a function of
is considered as a function of 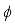 instead of
instead of 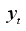 , it is referred to as the likelihood function. By applying Bayes' theorem, the posterior pdf
, it is referred to as the likelihood function. By applying Bayes' theorem, the posterior pdf 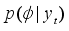 can be derived, that is, the posterior pdf of
can be derived, that is, the posterior pdf of 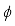 given
given 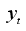 , by multiplying the likelihood with the prior density,
, by multiplying the likelihood with the prior density, 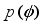 . That is,
. That is, 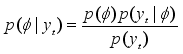 (4)
(4) 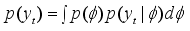
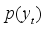 defines what is known as predictive density function. The prior distribution provides a means to include researcher's initial beliefs or assumptions regarding
defines what is known as predictive density function. The prior distribution provides a means to include researcher's initial beliefs or assumptions regarding 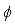 , and Bayes' theorem enables the revision and updating of these assumptions once the data is observed.
, and Bayes' theorem enables the revision and updating of these assumptions once the data is observed. 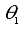 and
and 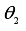 are taken as independent and normally distributed as
are taken as independent and normally distributed as 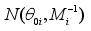 , while
, while 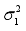 and
and 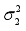 are taken as independent with inverse gamma distribution inverse gamma
are taken as independent with inverse gamma distribution inverse gamma 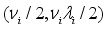 . The hyper-parameters d and r are assumed to be known. r is presumed to have a uniform distribution on
. The hyper-parameters d and r are assumed to be known. r is presumed to have a uniform distribution on 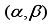 while d is presumed to take a discrete uniform distribution on 1,2,..., D.
while d is presumed to take a discrete uniform distribution on 1,2,..., D. 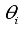 's,
's, 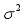 s, r, and d. Determining the posterior distribution is frequently achallenging task due to the need for complex numerical integration in high-dimensional spaces. Therefore, Gibbs Sampler and the Metropolis-Hastings algorithm will be used in this study to find the conditional posterior distributions of the unknown parameters.
s, r, and d. Determining the posterior distribution is frequently achallenging task due to the need for complex numerical integration in high-dimensional spaces. Therefore, Gibbs Sampler and the Metropolis-Hastings algorithm will be used in this study to find the conditional posterior distributions of the unknown parameters. 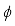 can be broken down into components
can be broken down into components 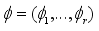 and the conditional densities
and the conditional densities 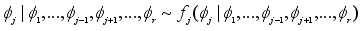 can be simulated for
can be simulated for 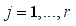 . Then, to sample from the joint density of
. Then, to sample from the joint density of 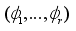 using Gibbs sampler, the following algorithm is followed:
using Gibbs sampler, the following algorithm is followed: 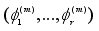 , generate
, generate 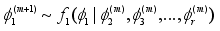 ,
, 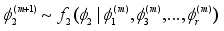 ,
, 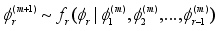 .
. 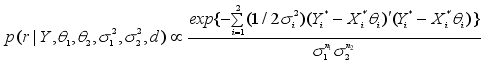 (5)
(5) 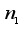 and
and  being functions of r.
being functions of r. 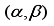 is made. Hence, a transition kernel
is made. Hence, a transition kernel 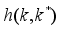 with
with 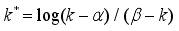 can be utilized to map
can be utilized to map 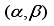 into
into 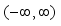 . The Metropolis algorithm will then work in the following manner;
. The Metropolis algorithm will then work in the following manner; 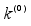 drawn from the prior
drawn from the prior 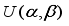 and set the indicator
and set the indicator 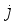 to 0.
to 0. 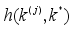 , generate a new point
, generate a new point 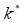 .
. 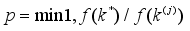 , update
, update 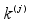 to
to 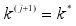 and remain at
and remain at 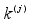 with a probability of
with a probability of 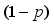 .
. 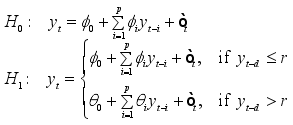 (6)
(6) 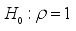 (hasunitroots)
(hasunitroots) 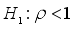 (nounitroots)
(nounitroots) 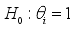 (serieshasaunitrootwithdrift)
(serieshasaunitrootwithdrift) 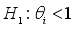 (seriesisstationarywithbreak(s))
(seriesisstationarywithbreak(s)) 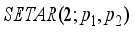 .
. 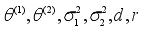 are estimated using the Bayesian approach. The Gibbs sampler was executed for 1,000 iterations, and the initial 500 iterations were disregarded as the burn-in sample. The estimates of the parameters alongside their standard errors are as shown in the table below;
are estimated using the Bayesian approach. The Gibbs sampler was executed for 1,000 iterations, and the initial 500 iterations were disregarded as the burn-in sample. The estimates of the parameters alongside their standard errors are as shown in the table below; 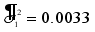 and
and 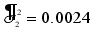 . The estimated value of d is 1.
. The estimated value of d is 1.