Abstract: Suppose that

is a real or complex unital Banach *-algebra,
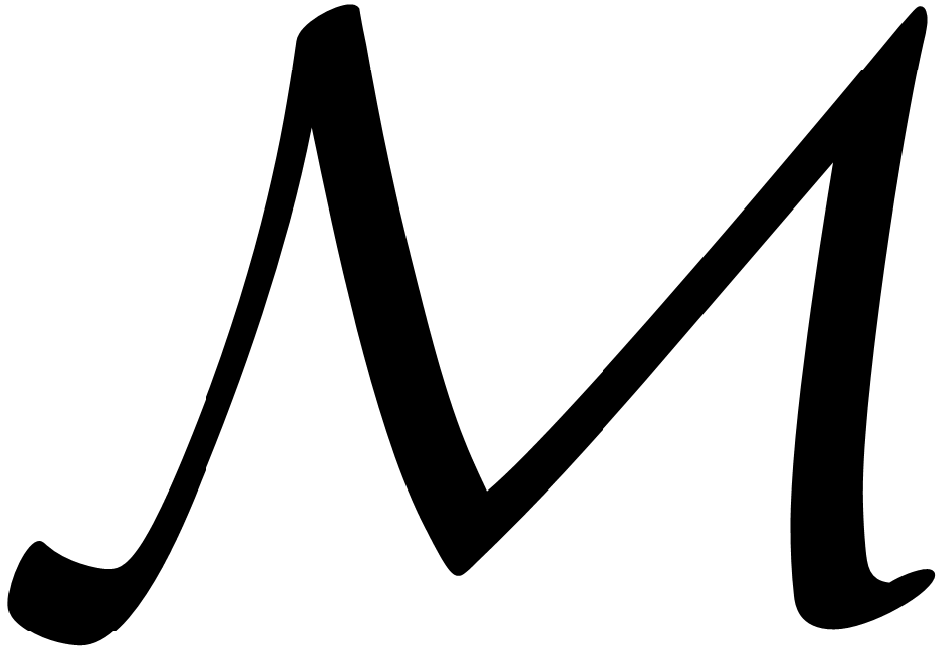
is a unital Banach

-bimodule, and G ∈

is a left separating point of
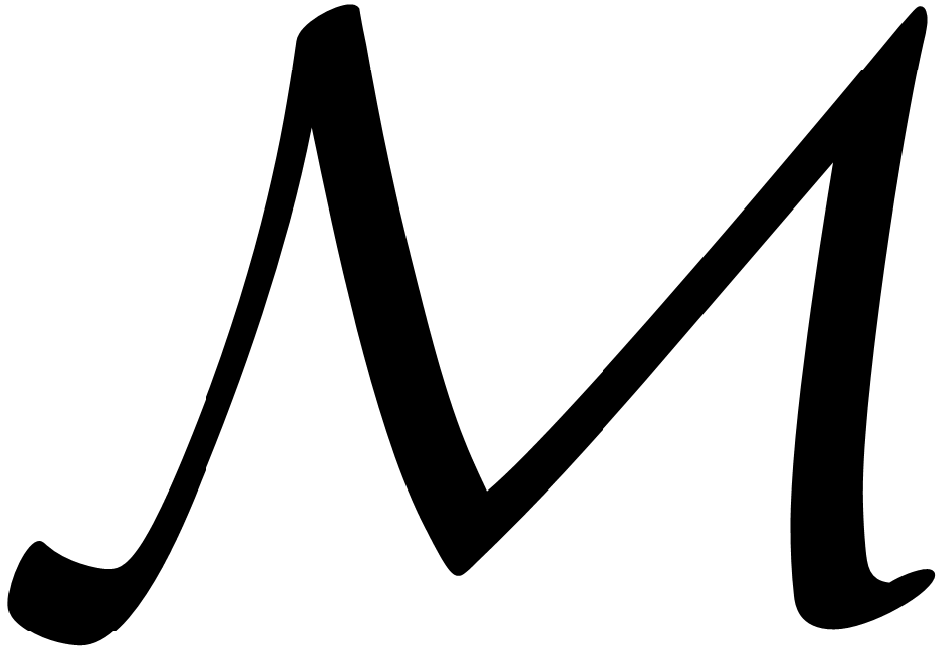
. In this paper, we investigate whether the additive mapping
δ:

→
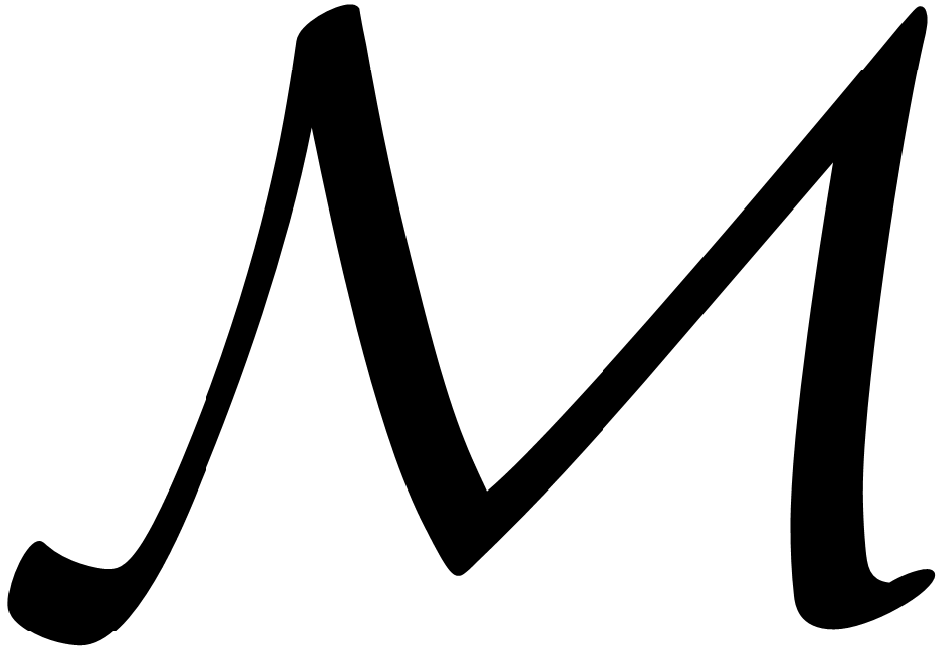
satisfies the condition
A,B ∈

,
AB = G ⇒
Aδ(
B)+
δ(
A)
B*=
δ(G) characterize Jordan
*-derivations. Initially, we prove that if

is a real unital
C*-algebra and
G =
I is the unit element in

, then
δ (non-necessarily continuous) is a Jordan
*-derivation. In addition, we prove that if

is a real unital
C*-algebra and
δ is continuous, then
δ is a Jordan
*-derivation. Finally, we show that if

is a complex factor von Neumann algebra and
δ is linear, then
δ (non-necessarily continuous) is equal to zero.


