Search engines have become crucial tools today, providing users with access to vast amounts of information. At the core of search engine functionality lies the ranking algorithm, which is responsible for determining the relevance and order of web pages returned in response to user queries. Ranking algorithms play a critical role in ensuring that users receive the most relevant and useful results, particularly in the face of exponentially growing web content. This paper provides an in-depth analysis of PageRank algorithms, focusing on their significance in information retrieval systems. The study begins with an overview of the foundational PageRank algorithm developed by Google, detailing its reliance on hyperlink structures to rank web pages. The limitations of the original algorithm, such as its inability to consider page content relevance and dynamic updates, are explored. In response to these limitations, the paper examines advanced ranking methods, including the Weighted PageRank (WPR), Hyperlink-Induced Topic Search (HITS), and the Stochastic System Analysis Approach (SALSA). Each of these algorithms is analyzed in terms of efficiency, response time, scalability, and effectiveness. Additionally, the paper investigates recent enhancements in ranking methods that address the evolving needs of modern search engines, such as personalized search and semantic relevance. Experimental comparisons are conducted to evaluate the performance of these algorithms on large-scale datasets. Key metrics, including time response, computational efficiency, and relevance accuracy, are used to compare and rank the algorithms. The findings provide valuable insights into the strengths and weaknesses of different PageRank methods, contributing to the development of more efficient and effective information retrieval systems.
| Published in | American Journal of Information Science and Technology (Volume 9, Issue 1) |
| DOI | 10.11648/j.ajist.20250901.12 |
| Page(s) | 15-23 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2025. Published by Science Publishing Group |
Information Retrieval, Web Page Ranking, Effectiveness, Efficiency, Search Engines
Iteration | PR (A) | PR (B) | PR (C) |
|---|---|---|---|
0 | 1 | 1 | 1 |
1 | 1.00 | 0.58 | 1.06 |
2 | 1.05 | 0.60 | 1.10 |
3 | 1.09 | 0.61 | 1.13 |
4 | 1.11 | 0.62 | 1.15 |
5 | 1.13 | 0.63 | 1.17 |
6 | 1.14 | 0.63 | 1.17 |
7 | 1.14 | 0.63 | 1.17 |
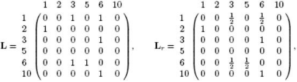




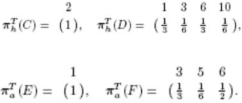


Algorithm | Advantages | Disadvantages |
|---|---|---|
PageRank | 1. Query time is less. 2. Feasibility As compared to another algorithms the PageRank algorithm is more feasible. | Relevancy to user’s requirements is Less |
Weighted PageRank | The Quality of the pages that is returned is more high than PageRank algorithm | This algorithm results also are less in relevancy to user’s requirements. |
HITS | 1. HITS returns in the appropriate authority and hub pages thanks to its ability to identify pages according to the question chain. 2. The rating may also be paired with other rankings dependent on knowledge set. 3. HITS is user-sensitive (in contrast with PageRank). | 1. Query Time Cost: Calculation of query time is costly. It is a big downside since HITS is an algorithm based on a question. 2. Important: the ranking or the number of authorities and hubs may increase due to the web page designer's failures. |
Stochastic Approach Forlink Structure Analysis (SALSA) | 1. SALSA is less vulnerable to the TKC effect, and produces good results in many cases where the mutual reinforcement approach fails to do so. 2. SALSA is particularly effective for very general queries. | Sometimes the effect is beyond mutual reinforcement Approach, and it prevents it from finding relevant trusted sites (or from finding authorities at all |
Algorithm | PageRank | Weighted PageRank | HITS | SALSA |
|---|---|---|---|---|
Technique | The Structure of web page | Based on Structure of web page | Web Structure Mining and Web Content Mining | analysis of the correlation structure of sub-web graphics. |
Working methodology | scores of pages are computed at indexing time | The web page waiting depends on in links and out links | Compute the Hubs and Authority | SALSA can be seen as an improvement of HITS. (finding hubs and authorities) |
Input Parameter | The back links | Forward links and the back links | Contents, Back link and forward links | Contents, Links |
Quality of results | Medium | More than Page rank algorithm | Less than page rank | SALSA computationally lighter than the Mutual Reinforcement approach |
Time | O (Log n) | < O (Log n) | <O (Log n) (higher than WPR) | O(N + E) |
Strength | Back links (in links) are very considered | The pages are sorted according to the weight of in links and out links | Moderate. Hub & authorities scores are utilized. | SALSA is particularly effective at scoring fairly general queries |
Weakness | Results generated at indexing time not query time, also inability to handle results by using natural language without keywords | Theme drift | Topic Drift and Efficiency | Relative position was not so effective |
Technique | Web Structure Mining | Web Structure Mining | Web Structure Mining and Web Content Mining | analysis of the correlation structure of sub-web graphics. |
| [1] | Manning, C. D., Raghavan, P., and Schutze, H., ‘Introduction to Information Retrieval’, Introduction to Information Retrieval, (2008). |
| [2] | ME, Mrs Mercy Paul Selvan, A. Chandra Sekar ME, and A. P. D., ‘Ranking Techniques for Social Networking Sites based on Popularity’, (2012). |
| [3] | Ridings, C., & Shishigin, M., ‘Pagerank uncovered. Technical Paper for the Search Engine Optimization Online Community’, (2002). |
| [4] | Grover, N. and Wason, R., ‘Comparative Analysis of Page Rank And HITS Algorithms’, International Journal of Engineering Research & Technology (IJERT), (2012). |
| [5] | Gupta, P., Goel, A., Lin, J., Sharma, A., Wang, D., and Zadeh, R., ‘WTF: The Who to Follow service at Twitter’, (2013). |
| [6] | Patel, P., ‘Research of Page ranking algorithm on Search engine using Damping factor’, International Journal Of Advance Engineering And Research Development, (2014). |
| [7] | Lempel, R. and Moran, S., ‘Stochastic approach for link-structure analysis (SALSA) and the TKC effect’, Computer Networks, (2000). |
| [8] | T. Mandl, “Artificial Intelligence for Information Retrieval,” Encyclopedia of Artificial Intelligence, Jan. 2011, |
| [9] | V. Rijsbergen, “Information Retrieval - Chapter 7,” Inf Retr Boston, pp. 112–140, 1979, Accessed: Nov. 12, 2024. [Online]. Available: |
| [10] | Y. Rochat, “Closeness Centrality Extended To Unconnected Graphs : The Harmonic Centrality Index,” ASNA, 2009. |
| [11] | S. Robertson and H. Zaragoza, “The probabilistic relevance framework: BM25 and beyond,” Foundations and Trends in Information Retrieval, vol. 3, no. 4, pp. 333–389, 2009, |
| [12] | H. Y. Modi and M. Narvekar, “A Comparative Study of Various Page Ranking Algorithms”, [Online]. Available: |
| [13] | S. Zhang, R. Yang, X. Xiao, X. Yan, and B. Tang, “Effective and Efficient PageRank-based Positioning for Graph Visualization,” Proceedings of the ACM on Management of Data, vol. 1, no. 1, pp. 1–27, Nov. 2023, |
| [14] | D. F. Gleich, “PageRank beyond the web,” SIAM Review, vol. 57, no. 3, 2015, |
| [15] | N. Grover and R. Wason, “Comparative Analysis of Pagerank And HITS Algorithms.” [Online]. Available: |
| [16] | M. Bianchini, M. Gori, and F. Scarselli, “Inside PageRank,” ACM Transactions on Internet Technology (TOIT), vol. 5, no. 1, pp. 92–128, Feb. 2005, |
| [17] | Mang’are Fridah Nyamisa, Waweru Mwangi, Wilson Cheruiyot. (2017). A Survey of Information Retrieval Techniques. Advances in Networks, 5(2), 40-46. |
APA Style
Edrees, Z., Juma, H. (2025). Comparative Analysis of Page Ranking Algorithms for Efficient Information Retrieval. American Journal of Information Science and Technology, 9(1), 15-23. https://doi.org/10.11648/j.ajist.20250901.12
ACS Style
Edrees, Z.; Juma, H. Comparative Analysis of Page Ranking Algorithms for Efficient Information Retrieval. Am. J. Inf. Sci. Technol. 2025, 9(1), 15-23. doi: 10.11648/j.ajist.20250901.12
AMA Style
Edrees Z, Juma H. Comparative Analysis of Page Ranking Algorithms for Efficient Information Retrieval. Am J Inf Sci Technol. 2025;9(1):15-23. doi: 10.11648/j.ajist.20250901.12
@article{10.11648/j.ajist.20250901.12,
author = {Zahir Edrees and Henda Juma},
title = {Comparative Analysis of Page Ranking Algorithms for Efficient Information Retrieval},
journal = {American Journal of Information Science and Technology},
volume = {9},
number = {1},
pages = {15-23},
doi = {10.11648/j.ajist.20250901.12},
url = {https://doi.org/10.11648/j.ajist.20250901.12},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajist.20250901.12},
abstract = {Search engines have become crucial tools today, providing users with access to vast amounts of information. At the core of search engine functionality lies the ranking algorithm, which is responsible for determining the relevance and order of web pages returned in response to user queries. Ranking algorithms play a critical role in ensuring that users receive the most relevant and useful results, particularly in the face of exponentially growing web content. This paper provides an in-depth analysis of PageRank algorithms, focusing on their significance in information retrieval systems. The study begins with an overview of the foundational PageRank algorithm developed by Google, detailing its reliance on hyperlink structures to rank web pages. The limitations of the original algorithm, such as its inability to consider page content relevance and dynamic updates, are explored. In response to these limitations, the paper examines advanced ranking methods, including the Weighted PageRank (WPR), Hyperlink-Induced Topic Search (HITS), and the Stochastic System Analysis Approach (SALSA). Each of these algorithms is analyzed in terms of efficiency, response time, scalability, and effectiveness. Additionally, the paper investigates recent enhancements in ranking methods that address the evolving needs of modern search engines, such as personalized search and semantic relevance. Experimental comparisons are conducted to evaluate the performance of these algorithms on large-scale datasets. Key metrics, including time response, computational efficiency, and relevance accuracy, are used to compare and rank the algorithms. The findings provide valuable insights into the strengths and weaknesses of different PageRank methods, contributing to the development of more efficient and effective information retrieval systems.},
year = {2025}
}
TY - JOUR T1 - Comparative Analysis of Page Ranking Algorithms for Efficient Information Retrieval AU - Zahir Edrees AU - Henda Juma Y1 - 2025/02/11 PY - 2025 N1 - https://doi.org/10.11648/j.ajist.20250901.12 DO - 10.11648/j.ajist.20250901.12 T2 - American Journal of Information Science and Technology JF - American Journal of Information Science and Technology JO - American Journal of Information Science and Technology SP - 15 EP - 23 PB - Science Publishing Group SN - 2640-0588 UR - https://doi.org/10.11648/j.ajist.20250901.12 AB - Search engines have become crucial tools today, providing users with access to vast amounts of information. At the core of search engine functionality lies the ranking algorithm, which is responsible for determining the relevance and order of web pages returned in response to user queries. Ranking algorithms play a critical role in ensuring that users receive the most relevant and useful results, particularly in the face of exponentially growing web content. This paper provides an in-depth analysis of PageRank algorithms, focusing on their significance in information retrieval systems. The study begins with an overview of the foundational PageRank algorithm developed by Google, detailing its reliance on hyperlink structures to rank web pages. The limitations of the original algorithm, such as its inability to consider page content relevance and dynamic updates, are explored. In response to these limitations, the paper examines advanced ranking methods, including the Weighted PageRank (WPR), Hyperlink-Induced Topic Search (HITS), and the Stochastic System Analysis Approach (SALSA). Each of these algorithms is analyzed in terms of efficiency, response time, scalability, and effectiveness. Additionally, the paper investigates recent enhancements in ranking methods that address the evolving needs of modern search engines, such as personalized search and semantic relevance. Experimental comparisons are conducted to evaluate the performance of these algorithms on large-scale datasets. Key metrics, including time response, computational efficiency, and relevance accuracy, are used to compare and rank the algorithms. The findings provide valuable insights into the strengths and weaknesses of different PageRank methods, contributing to the development of more efficient and effective information retrieval systems. VL - 9 IS - 1 ER -